

Ü And if you think Greeks invented calculus? No, they did not. It traveled as high up to its peak and is falling down, still the difference between its height at t=0 and t=1 is 4ft. Bear in mind that the ball went much farther. The height of the ball, 1 second later, will be 4 feet high above the original height. Therefore, if a ball is thrown upright into the air with velocity identify, and interpret, ∫10v(t)dt.Įxecuting the Second Fundamental Theorem of Calculus, we see Anie wins the race, but narrowly.Ī ball is thrown straight up from the 5 th floor of the building with a velocity v(t)=−32t+20ft/s, where t is calculated in seconds. That said, when we know what’s what by differentiating sin(π²t), we get π²cos(π²t) as an outcome of the chain theory, so we need to take into consideration this additional coefficient when we combine them. You recognize that sin ‘t’ is an antiderivative of cos, so it is rational to anticipate that an antiderivative of cos(π²t) would include sin(π²t). Now moving on to Anie, you want to evaluate Thus, Jessica has ridden 50 ft after 5 sec.

Find out who is going to win the horse race?įirst, you need to combine both functions over the interval (0,5) and notice which value is bigger. (Fundamental Theorem of Calculus Part 2) If f(x) is. If Jessica can ride at a pace of f(t)=5+2t ft/sec and Anie can ride at a pace of g(t)=10+cos(π²t) ft/sec. We can however use FTC Part 1 to determine a way to calculate definite integrals exactly. They are riding the horses through a long, straight track, and whoever reaches the farthest after 5 sec wins a prize. The fundamental theorem of Calculus states that if a function f has an antiderivative F, then the definite integral of f from a to b is equal to F(b)-F(a). Two jockeys-Jessica and Anie are horse riding on a racing circuit.
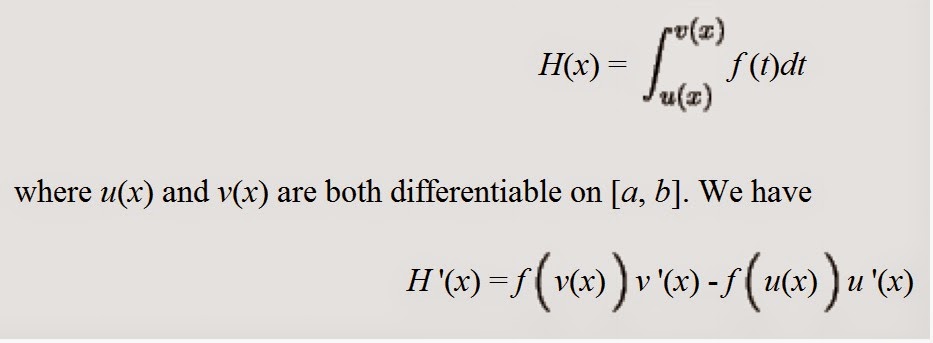
Using First Fundamental Theorem of Calculus Part 1 Example Lower limit of integration is a constant. \ĭerivative matches the upper limit of integration. The Fundamental Theorem of Calculus denotes that differentiation and integration makes for inverse processes. If F is integrable on a,b, then baF(x)dxF(b)F(a). However, what creates a link between the two of them is the fundamental theorem of calculus (FTC). Theorem (FTC part 2): Let F be continuous on a,b and differentiable on (a,b). The Fundamental Theorem of Calculus, Part 2 (also known as the evaluation theorem) states that if we can find an antiderivative for the integrand, then we can. Both are inter-related to each other, even though the former evokes the tangent problem while the latter from the area problem. – differential calculus and integral calculus. There are 2 primary subdivisions of calculus i.e. This reminds us of the property that the difference between any 2 antiderivatives of a function is a constant see. In this case, t is simply a placeholder that allows us to avoid confusion that could otherwise result from using x in both the bounds of the integral as well as the integrand since for all values of x, F(x) is dependent only on x, not t.Before proceeding to the fundamental theorem, know its connection with calculus. Note that even though F(x) is defined in terms of the integral of another function, which may seem confusing since we expect a definite integral to be a number, the result of the integral for any given x value is indeed a number. In other words, the area under the curve is represented by: In the figure, F(x) is a function that represents the area under the curve between a and some point x within the interval. We first note that we have already proven part 2 as Theorem 4.1. Given a function f(t) that is continuous over an interval, recall that an integral represents the area under the curve. We used the Fundamental Theorem of Calculus to evaluate definite integrals. It also gives us an efficient way to evaluate definite integrals. The fundamental theorem of calculus (FTC) establishes the connection between derivatives and integrals, two of the main concepts in calculus.
Home / calculus / integral / fundamental theorem of calculus Fundamental theorem of calculus


 0 kommentar(er)
0 kommentar(er)
